POWER POINT ON KINDS OF FORCE
1) the lift accelerates up with an acceleration
2m/s2
2) the lift accelerates down with an
acceleration of 5m/s2
3) the lift goes up with a constant velocity of
3m/s
16) a car moving at 25m/s collides with a wall and come to rest.The driver of mass 65 kg is brought to rest by his seat belt in 0.2 seconds.Calculate
1) the drivers change in momentum
2)the average force exerted by the seat belt on the driver..
17) Find the impulse and force which make 12m/s change in the velocity of object having 16kg mass in 4 s.
F.t=change in momentum = ΔP=m.(v-u)
F.4s=16kg.12m/s
F=48N
F.Δt=Impulse=192kg.m/s
Recoil of Gun
Mass of gun = M
Mass of bullet = m
Initially gun and the bullet are at rest.
Initial velocity of gun=0
initial velocity of bullet = 0
Therefore
The total initial momentum before firing
= M x 0+ m x 0 = 0
The bullet leaves the gun with a large velocity V. The gun recoils with a small velocity v
Final momentum of the gun after firing=Mv
Final momentum of the bullet after firing=mV
Total final momentum= Mv + mV
By law of conservation of momentum
total momentum before firing = total momentum after firing
0 = mV + Mv
Recoil velocity of gun = v= - mV/M
18) A bullet of mass 20g leaves a gun of mass 1.5kg with a velocity 50m/s.Calculate the recoil velocity of the gun.
Total momentum before firing = total momentum after firing
0 + 0 = mV + Mv
0 = 0.02 x 50 + 1.5 x v
0= 1+1.5 v
v= - 1/1.5m/s
19) A 25 gram bullet is fired from a gun with a speed of 230m/s. If the gun has a massof 0.9kg. what is the recoil speed of the gun?
21) A 0.60kg glider traveling at 8.0 m/s on a level air track undergoes a head-on collision with a 0.20kg mass glider traveling toward it at 4.0 m/s. The two gliders stick in the collision. What is the velocity of the combined gliders after the collision?
22) A glider with mass m and speed v moving along an air track collides with a stationary cart with a mass m/3. After the collision the first cart has a speed v/2. What is the velocity of the second cart?
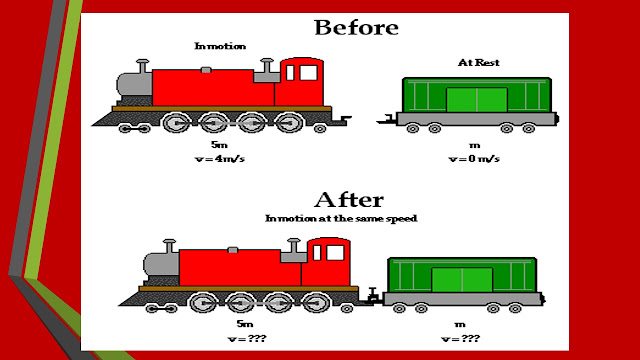
23) A 12,000kg. railroad car is traveling at 2m/s when it strikes another 10,000kg.railroad car that is at rest. If the cars lock together, what is the final speed of the two railroad cars?
LAW OF CONSERVATION OF MOMENTUM AND COLLISIONS
https://www.youtube.com/watch?v=2E9fY8H6O1g
https://www.youtube.com/watch?v=XFmbB4bMDEA
Q24)
Q26)
Q33)A car of 500 kg, traveling at 30 m/s rear ends another car of 600 kg, traveling at 20 m/s in the same direction The collision is great enough that the two cars stick together after they collide. How fast will both cars be going after the collision?
Q34)A block of mass 2kg is pushed along
a table with a constant velocity by a force
of 5N.When push is increased to 9Nwhat is a)the resultant force
b) the acceleration
35) What does an astronaut of mass 100kg weigh a) on earth where the acceleration due to gravity is 10m/s2
b) On moon where the g= 1.6m/s2.
36) a rocket has a mass of 500kg.
a) What is the weight on earth where g=10m/s2 b) at lift off the rocket engine exerts an upward force of 25000N .What is the resultant force
on the rocket?What is its initial acceleration ?
37) Explain using F=ma
a) a racing car has a powerful engine and is made of strong but light weight material.
b) Car with small engine can accelerate rapidly
38)A ball X of mass 1kg travelling at 2m/s has a head on collision with an identical ball Y at rest.X stops and Y moves off .What is the velocity of Y?
39) A boy of mass 50 kg is standing in a lift.
Calcuate the apparent weight of the boyif
a) the lift is at rest
b) lift goes up with constant velocity
c) lift goes down with constant velocity
d) lift goes up with acceleration 1.5m/s2
e) lift goes downwith acceleration 2.5m/s2
Numerical
Problems
Force and
Newton's Law of Motion, Class 11
Ex.1 Calculate the force required to impact to a car, a velocity of 30 m
s_1 in 10 seconds if the car is initially at rest. The mass of the
car is 1,500 kg.
Sol. Here u = 0 m s_1; v = 30 ms_1; t = 10 s; a = ?
Using v = u at, we have
30 = 0 a (10)
a = 3 m s_2
Now F = ma = 1,500 × 3
or F = 4,500 N
Ex.2 A cricket ball of mass 70 g moving with a velocity of 0.5 m s_1
is stopped by player in 0.5 s. What is the force applied by player to stop the ball
?
Sol. Here m = 70 g = 0.070 kg; u = 0.5 m s_1; v = 0; t = 0.5 s
F = 
or F = 
or F = _ 0.07 newton
Ex.3 What will be acceleration of a body of mass 5 kg if a force of 200 N
is applied to it ?
Sol. Here m = 5 kg; F = 200 N
F = ma or a = F/m
a = 
=
40 m s_2
=
40 m s_2
a = 40 m s_2
Ex.4 A bullet of mass 10 g is fired from a rifle. The bullet takes 0.003
s to move through its barrel and leaves with a velocity of 300 m s_1.
What is the force exerted on the bullet by the rifle?
Ex.5 What force would be needed to produce an acceleration of 1 m s_2
on a ball of mass 1 kg ?
Sol. Here m = 1 kg; a = 1 m s_2 ; F = ?
Now F = m a = 1 × 1
or F = 1 newton
Ex.6 What is the acceleration produced by a force of 5 N exerted on an
object of mass 10 kg ?
Sol. Here F = 5 N; m = 10 kg; a = ?
Now F = ma or a =
a = = 0.5 m s_2
Ex.7 How long should a force of 100 N act on a body of 20 kg so that it
acquires a velocity of 100 m s_1 ?
Sol. Here v _ u = 100 m s_1, m = 20 kg; F = 100 N ;t = ?
We know F = ma =
or t = 
=
20 s
=
20 s
Ex.8 A 1,000 kg vehicle moving with a speed of 20 m s_1 is
brought to rest in a distance of 50 m, (i) Find the acceleration; (ii)
Calculate the unbalanced force acting on the vehicle; (iii) The actual force
applied by the brakes may be slightly less than that calculated in (ii). Why?
Give reason.
Sol. (i) Here u = 20 m s_1; v = 0; s = 50 m; a = ?
Using v2 _ u2 = 2as, we have
a = 
=
_4 ms_2
=
_4 ms_2
(ii) F = ma = 1,000 × (_4) = _4,000 N
(iii) Due to force of friction, the actual force applied by brakes may
be slightly less than calculated one.
Ex.9 Which would require greater force: accelerating a 10 g mass at 5 m s_2
or 20 g mass at 2 m s_2?
Sol. In first case m1 = 10 g = kg = 0.010 kg;
Now a1 = 5 ms_2 ; F1 = ?
F1 = m1a1 = 0.010 × 5
F1 = 0.050 newton
In second case, m2 = 20 g = kg
or m2 = 0.020 kg
a2 = 2 m s_2 ; F2 = ?
Now F2 = m2a2 = 0.020 × 2
or F2 = 0.04 newton
We find that F1 > F2, hence more force is
required to accelerate 10 g at 5 m s_2 than accelerating 20 g at 2 m
s_2.
Ex.10 A truck starts from rest and rolls down a hill with constant
acceleration. It travels a distance of 400 m in 20 s. Find its acceleration.
Find the force acting on it if its mass is 7 metric ton.
Sol. Here u = 0 m s_1 (Starting from rest); s = 400 m; t = 20 s;
a = ?
Using s = ut at2,
We have 400 = 0 × a × 20 × 20 = 200 a
or a = 2 m s_2
Now mass m = 7 metric ton = 7,000 kg; F = ?
F = m a = 7,000 × 2
or F = 14,000 N
Ex.11 A force of 5 N gives a mass m1, an acceleration of 8 m s_2
and a mass m2, an acceleration of 24 m s_2. What
acceleration would it give if both the masses are tied together?
Sol. Let us first find mass m1 and m2.
F = m1 a1
5 =m1 (8) or m1 = 5/8 kg
F = m2 a2
5 = m2 (24) or m2 = 5/24 kg
Total mass M = m1 m2
or M = 
or M = 
kg
kg
Let A be the acceleration produced in mass M.
F = MA
or 5 = A
A
or A = 
=
6 ms_2
=
6 ms_2
Hence the acceleration of the combination is 6 m s_2.
Ex.12 A car of mass 1,000 kg moving with a velocity of 40 km h_1
collides with a tree and comes to stop in 5 s. What will be the force exerted
by car on the tree ?
Sol. Here m = 1,000 kg
u = 40 × ms_1 = ms_1
v = 0 ; t = 5 s
F =
or F =
or F = 200 
or F = 
or F = _2,222 N
Ex.13 The velocity-time graph of a coin moving on a floor is as given in
Fig. How much force does the floor exert on the coin? Given the mass of the
coin is 10 g.
Sol. Here, u = 24 cm s_1
v = 0 m s_1; t = 8 s ; a = ?
v = u at
F = m a;
Here m = 10 g
F = 10 (_3) = _ 30 dyn = _ 30/(105) N
or F = _3 × 10_4 N.
Negative sign tells us that the force is acting in the direction
opposite to the direction of motion.
Ex.14 A bullet of mass 100 g is fired from a gun of mass 20 kg with a
velocity fo 100 ms1. Calculate the velocity of recoil of the gun.
Sol. Mass of bullet, m = 100 g = 
kg
= kg
kg
= kg
Velocity of bullet, u = 100 ms1
Mass of gun, M = 20 kg
Let recoil velocity of gun = V
Step 1. Before firing, the system (gun bullet) is at rest, therefore, initial
momentum of the system = 0
Final momentum of the system = momentum of bullet momentum of gun.
= mu MV = × 100 20 V = 10 20 V
Step 2. Apply law of conservation of momentum
Final momentum = Initial momentum
i.e. 10 20 V = 0
20 V = 10
or V = = 0.5 ms1.
Negative sign shows that the direction of recoil velocity of the gun is
opposite to the direction of the velocity of the bullet.
Ex.15 An iron sphere of mass 10 kg is dropped from a height of 80 cm. If
the downward acceleration of the ball is 10 ms2, calculate the
momentum transferred to the ground by the ball.
Sol. Here, Initial velocity of sphere, u = 0
Distance travelled, s = 80 cm = 0.8 m
Acceleration of sphere, a = 10 ms2
Step 1. Final velocity of sphere when it just reaches the ground can be
calculated using
u2 u2 = 2as
u2 0 = 2 × 10 ms2 × 0.8 m = 16 m2s2
or u = 
=
4 ms1.
=
4 ms1.
Momentum of the sphere just before it touches the ground = mu = 10 kg ×
4 ms1 = 40 kg ms1
Step 2. On reaching the ground, the iron sphere comes to rest, so its final
momentum = 0
According to the law of conservation of momentum,
Momentum transferred to the ground = momentum of the sphere just before
it comes to rest
= 40 kg ms1.
= 40 kg ms1.
Ex.16 Two small glass spheres of masses 10 g and 20 g are moving in a
straight line in the same direction with velocities of 3 ms1 and 2
ms1 respectively. They collide with each other and after collision
glass sphere of mass 10 g moves with a velocity of 2.5 ms1. Find the
velocity of the second ball after collision.
Sol. Here, m1 = 10 g = kg = 102 kg
m2 = 20 g = 2 × 102 kg
u1 = 3 ms1 ; u2 = 2 ms1
u1 = 2.5 ms1 ; u2 = ?
Momentum of first sphere before collision = m1u1 =
102 kg × 3 ms1 = 3 × 102 kg ms1
Momentum of second sphere before collision = m2u2
= 2 × 102 kg × 2 ms1 = 4 × 102 kg ms1
Total momentum of both the spheres before collision = m1u1
m2u2
= 3 × 102 kg ms1 4 × 102 kg ms1
= 7 × 102 kg ms1
Now, momentum of first sphere after collision = m1u1
= 102 kg × 2.5 ms1 = 2.5 × 102 kg ms1
Momentum of second sphere after collision = m2u2
= 2 × 102 kg × u2 ms1 = 2 × 102
u2 kg ms1
Total momentum of both the spheres after collision=m1u1
m2u 2=2.5× 102 kgms1 2× 102u2kgms1
Now, according to the law of conservation of momentum.
Total momentum after collision = Total momentum before collision
2.5 × 102 2 × 102 u2 = 7 × 102
or 2 × 102 u2 = 7 × 102 2.5 × 102
No comments:
Post a Comment