Grade11: SEMESTER 1 CHAPTER 2 KINEMATICS

Problem 1: An object moves from point A to point B to point C, then back to point B and then to point C along the line shown in the figure below.

a) Find the distance covered by the moving object.

b) Find the magnitude and direction of the displacement of the object.

Solution to Problem 1:

a) distance = AB + BC + CB + BC = 5 + 4 + 4 + 4 = 17 km

b) The magnitude of the displacement is equal to the distance between the final point C and the initial point A = AC = 9 km

The direction of the displacement is the direction of the ray AB.

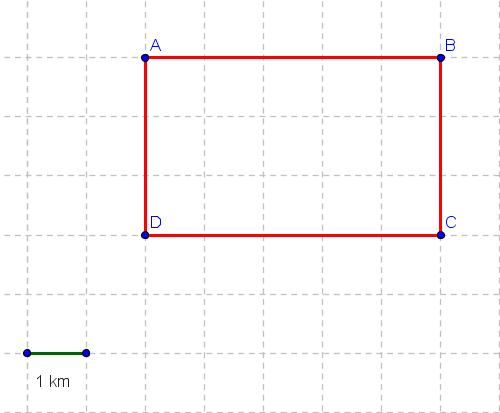
Problem 2: An object moves from point A to point C along the rectangle shown in the figure below.

a) Find the distance covered by the moving object.

b) Find the magnitude of the displacement of the object.

displacement and distance - Problem 2

Problem 3: An object moves from point A to B to C to D and finally to A along the circle shown in the figure below.
a) Find the distance covered by the moving object.
b) Find the magnitude and direction of the displacement of the object.

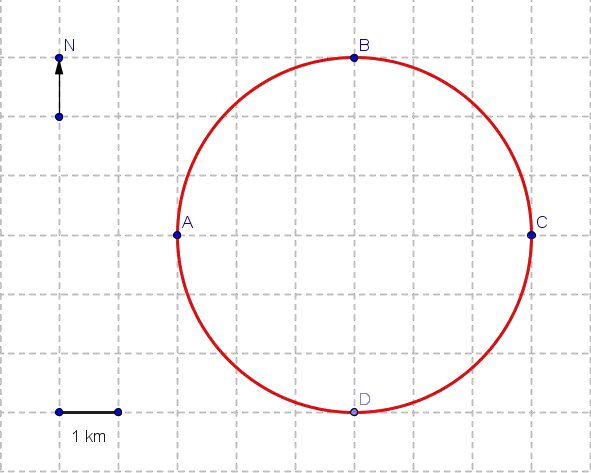
displacement and distance - Problem 3

Solution to Problem 3:
a) The object moves one complete rotation and therefore the distance d is equal to the circumference and is given by
d = 2 Pi * radius = 6 Pi km
b) Initial point is A and the final point is A, no change in position; hence the magnitude of the displacement is equal to zero

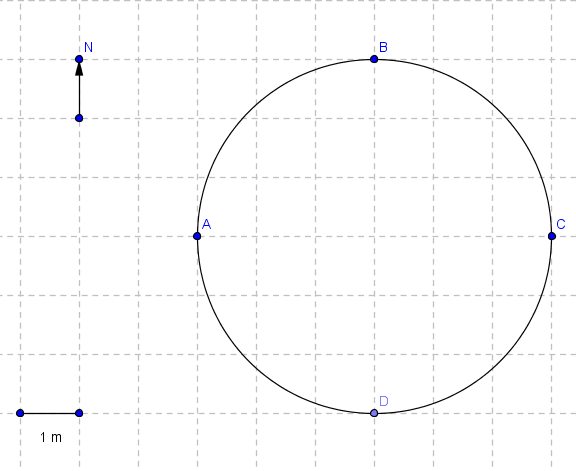
Problem 4: An object moves from point A to B to C to D along the circle shown in the figure below.

a) Find the distance covered by the moving object.

b) Find the magnitude of the displacement of the object.

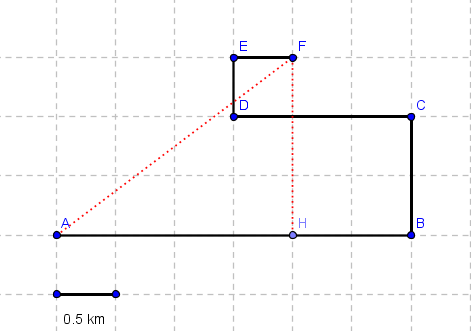
Problem 5: An object moves along the grid through the points A, B, C, D, E, and F as shown below.

a) Find the distance covered by the moving object.

b) Find the magnitude of the displacement of the object.

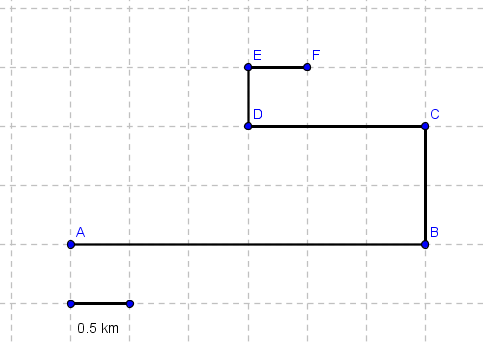
displacement and distance - Problem 5

Solution to Problem 5:

a) distance = AB + BC + CD + DE + EF = 3 + 1 + 1.5 + 0.5 + 0.5 = 6.5 km

b) Initial point is A and the final point is F, hence the magnitude of the displacement is equal to the distance AF which is calculated by applying Pythagora's theorem to the triangle AHF as shown in the figure below

www.dpisd.org/.../Distance-Displacement-Velocity%20Practice%20Probl...-

http://www.newarkcatholic.org/wp-content/uploads/2014/10/Distance-and-Displacement-Pkt-Key.pdf

http://www.problemsphysics.com/mechanics/motion/velo_spe_solutions.html

Q6)At an average speed of 24km/h how many kilometres will a cyclist travel in 75minutes?

Q7) A sprinter starting from the blocks reaches his full speed of 9m/s in 1.5s . What is his average acceleration?

EQUATIONS OF MOTION

1. v= u+at

2. s = ut +1/2 at²

3. v² = u²+ 2aS

U= initial velocity

V=final velocity

V_av= Average velocity

a= acceleration

s= displacement

t = time

Derive v = u+at

By definition
acceleration=change in velocity/time

a =( v-u)/t cross multiplying

at = v-u rearranging

v = u + at

Derive s = ut +1/2 at²

By definition,

average velocity = displacement/time

V_av = s/t There fore s = V_{av x} t ---- eq. 1

average velocity is also equal to

V_av = (u+v)/2---- eq. 2

V_av = {u+(u+at)}/2 = (2u+at)/2 ------eqn.3

comparing eqns 1 and 3

V_av = s/t =(2u+at)/2 cross multiplying 2s= 2ut + at²

s=( 2ut+at² )/2 = ut+1/2 a t²

s = ut+1/2 a t²

Derive v² = u²+ 2aS

By definition

average velocity = displacement/time

V_av = s/t-- eqn1

Also average velocity V_av = (u+v)/2 --------- eqn 2

comparing eqns 1 and 2 s/t =(u+v)/2

cross multiplying 2 x S =t x (u+v)

But t = (v-u)/a

2S = (v-u)/a x (u+v)

2s = (v² - u²)/across multiplying

v²- u² = 2aS

v² = u² +2aS

EQUATIONS OF MOTION
Problemshttp://www.physicsclassroom.com/class/1DKin/Lesson-6/Sample-Problems-and-Solutions

FREE FALL -Abody which isfalling freely only under the force of gravity is said to be in free fall.

g = 9.8m/s2

a= +9.8m/s2 if the body is falling down and
a = -9.8m/s2 if the body is going up

Q10) A stone is thrown up with a speed of 4m/s. calculate

a)how high it will rise and

b) the time taken for reaching the maximum height.(g=9.8m/s2)

Q11) A stone thrown up reaches the maximum height in 5seconds.

Calculate the velocity with which it is thrown up and the height it has reached.

Q12) A cricketer throws a ball vertically upward in to the air with an

initial velocity of 18m/s.

a)How high will it rise?

b)After how long will it return to the cricketer's hand?

Q13) A cricket ball is thrown vertically upwards with a speed of 15m/s.

What is the velocity when it passes throuh a point 8m bove the cricketers

hand?

Q14)

Q15)

https://www.khanacademy.org/math/cc-eighth-grade-math/cc-8th-linear-equations-functions/8th-slope/v/slope-of-a-line

http://farside.ph.utexas.edu/teaching/301/lectures/node20.html

http://www.physicsclassroom.com/morehelp/graphs

Area under velocity -Time graph gives displacement.

Q16)Calculte the displacement of the body from the velocity -time graph given below.

Q17)The velocity -Time graph of a body is given below. Calculate the total distance and the displacement of the body

The area under the velocity - time graph gives the displacement

Q18) The graph shows the motion of a lift starting at rest and initially moving upwards.

a) What is the overall displacement from the starting point by the end of the motion?
b) How high is the lift above the starting point at C?
c) What happens to the lift between Band C?
d) What happens to the lift between Dand F?
e) What is the acceleration of the lift between O and A?
Q19)

Q20) The figure below shows the velocity - time graph of a body.

a) What is the nature of motion represented by the following portions?
1) OA
2) AB
3) BC
4) CD
5) DE
b) The upward deceleration of the lift
c) the distance the lift moved in the upward direction
d) the distance the lift moved in the downward direction
e) Total distance covered
f) displacement of the lift
Q21)